This was a term-long school assignment, during fall of 2015. It was an opportunity to explore a wide range of concepts, many of which were completely new to me.
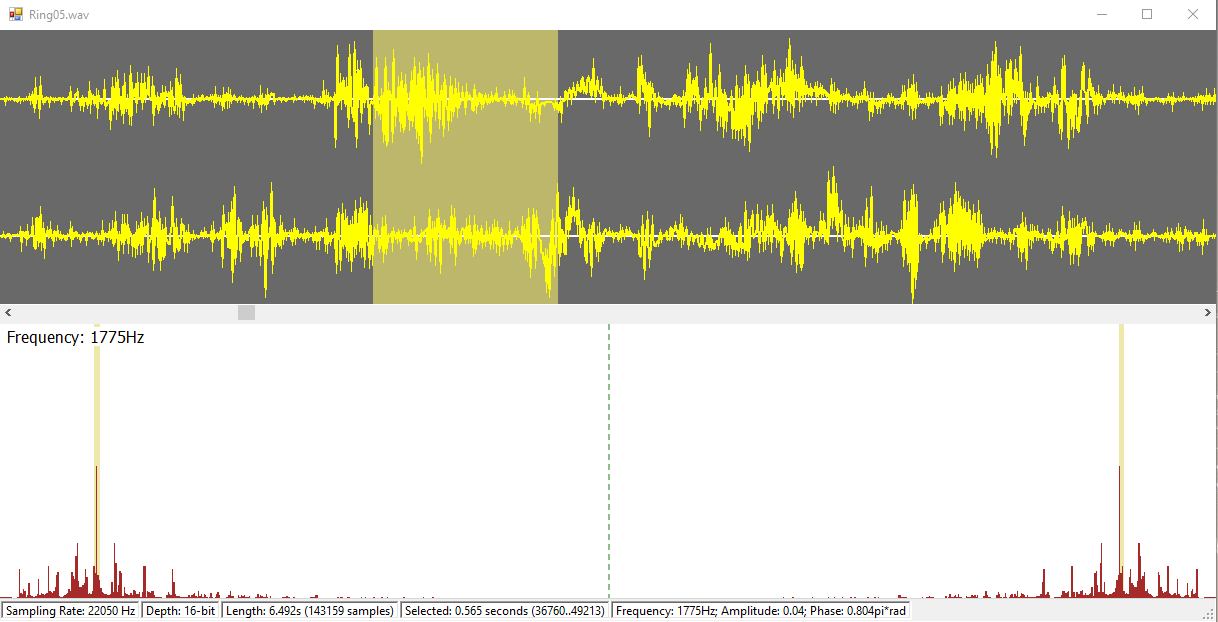
The complete program allowed a user to open, create, edit and save audio files. Within the application you can view the waveform and frequencies, and select time ranges, and then cut, copy and paste samples. With some samples selected you can amplify them, reverse them, and even change the pitch for some fun effects. You can change sampling rate and bit rate too.
By the end of this project I had my first programming experience in:
- Low-level Win32 multimedia functions WaveIn* and WaveOut*
- The C# Language
- Integrating Win32 dlls with C# code. That was a doozy to figure out!
- The Windows clipboard
These were just the programming tasks though. On a more fundamental level, I learned:
- Discrete Fourier Transform
- Forwards and inverse. There was a fun question on the final exam for this course where if you had a black-box function that performed a forward Fourier transform, but no inverse transform, could you use it to convert frequency domain information back to time? How? I’ll just leave it unanswered here!
- Filtering Audio
- Using different methods there are trade-offs of speed, precision, and frequency ripples. We talked about a variety of methods, but what I ended up including was filtering by Fourier transform, convolution, and infinite impulse response. It’s so cool—and honestly a little mind boggling—that with the impulse response filters you can take as few as three samples and still do a decent approximation of a highpass or lowpass filter.
- Windowing
- Windowing your samples is needed because Fourier’s equation assumes that a given set of samples is periodic. This can be problematic when viewing a small portion of a larger wave where the start and end don’t match (i.e. a high frequency is assumed). Windowing tries to bring the ends to the same amplitude and reduce surprise frequencies, but for the purposes of this program I just used windowing on the Fourier visualization.
- Time/Pitch Shifting
- This was an extra I added just for giggles. You can perform pitch-shifting of audio samples by playing them at slower or faster rates. Regrettably my computer won’t let me play a 22,050Hz sample at 21,200Hz, so we do something a little more creative. You can achieve the same pitch shifting effect—and keep your same sample rate—by a 3-step process:
- Insert a number N samples between every sample you currently have. (these can be anything but might as well be equal to what sample they proceed after.
- Low-pass filter your samples to turn the stair-step waves created by step 1 back into smooth curves.
- Keep only every D sample in your samples and discard the rest.
The complete project is hosted on on GitHub, with a small description of how to use it.